In questo articolo andremo ad analizzare la formula della potenza utile generata da un motore a 2 o 4 tempi.
La formula parte dall’Adamo ed Eva della termodinamica, ossia il principio di conservazione dell’energia (che non è altro che il primo principio della termodinamica). Lo sviluppo di questo principio porta, in pochi passi, ad una delle formule più affascinanti della meccanica: la formula della potenza.
Essa riassume quello che accade, nel bene e nel male, all’interno del motore ossia la generazione di POTENZA (il bene) e di CONSUMO SPECIFICO (il male). Tutto questo è contenuto in 16 termini che rendono la formula una “eccellente guida per il pensiero” [1]. Il massimo che posso fare per rendere onore a questa affascinante formula è quella di prendere la tavoletta grafica e scrivere, con la mia calligrafia da scaricatore di porto, ogni singolo passaggio matematico. Il buon proposito è quello, nel futuro, di poter dare una descrizione di ogni singolo termine, 16 pillole che possano stimolare la curiosità e portare il lettore ad approfondire la materia su alcuni testi sacri di cui parleremo nei prossimi mesi.
Iniziamo dal bilancio energetico (per ogni ciclo): nel cilindro entra il calore totale Qt e dall’albero motore esce il lavoro utile Lu.
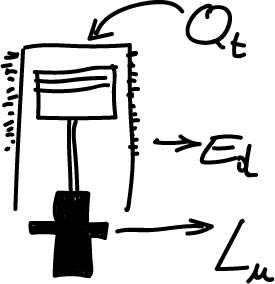
Dal cilindro viene dissipata, per ogni ciclo, una quantità di energia pari ad Ed. Questa è dovuta principalmente a:
- riscaldamento del fluido operante: aria a combustibile entrano nel cilindro ad una certa temperatura ed escono in forma gassosa (gas combusti) ad un temperatura maggiore;
- calore ceduto al liquido refrigerante attraverso le pareti del cilindro;
- calore corrispondente ad una difettosa combustione del combustibile dentro il cilindro;
- calore corrispondente al combustibile rifiutato all’aspirazione o espulso dallo scarico;
- irraggiamento e convezione del motore che si trova ad una temperatura superiore rispetto all’ambiente esterno.
Quindi il lavoro utile viene calcolato come:![]()
(1)
Definiamo adesso il rendimento termico utile come il rapporto tra lavoro utile (fornito all’albero motore) e l’energia termica (spesa ad ogni ciclo):
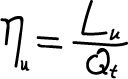 (2)
(2)
La potenza utile fornita da un singolo cilindro è data dal prodotto del lavoro utile per il numero di cicli compiuti dal motore in un secondo:
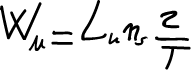 (3)
(3)
Dove:
è il numero di giri.
- T è il numero di “tempi” (2 o 4 tempi): se T=2, il T/2 vale 1 ossia il motore ha un ciclo attivo per ogni giro.
Partendo dalla (2) esprimiamo il lavoro utile come:
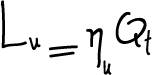 (4)
(4)
Definiamo adesso la massa di aria totale come la massima massa di aria che entra nel cilindro ignorando quello che viene rifiutata sull’aspirazione o espulsa dallo scarico.
Analogamente definiamo la massa di combustibile totale come la massa totale di combustibile spesa ad ogni ciclo indipendentemente dalla quantità che viene rigettata all’aspirazione o espulsa incombusta allo scarico:
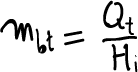 (5)
(5)
dove è il potere calorifico inferiore del combustibile.
Coerentemente definiamo il rapporto aria/combustibile totale come rapporto tra le due precedentemente citate masse (aria totale e combustibile totale):
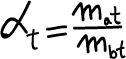 (6)
(6)
Definiamo adesso la massa di aria ideale la massa di aria che riempie completamente il cilindro, ed avente densità corrispondente alle condizioni nell’ambiente di aspirazione:
![]() (7)
(7)
dove è il volume del cilindro e
è la densità dell’aria.
Dividendo la massa di aria totale (7) per il rapporto aria/combustibile totale (6) troveremo la massa di combustibile ideale:
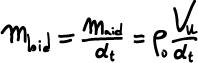
(8)
Moltiplicando la massa sopra citata per il potere calorifico si ottiene il calore ideale .
Definiamo adesso il rendimento volumetrico totale come il rapporto tra la massa di combustibile reale e ideale:
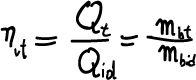
(9)
Applicando la (2), (5), (9) ed (8) alla (3) si ottiene la potenza utile erogata dal cilindro erogato:
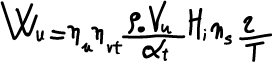
(10)
La vera grandezza importante è la velocità media dello stantuffo che andremo subito ad introdurre.
La relazione tra il regime d rotazione e velocità dello stantuffo
è:
(con
la corsa dello stantuffo).
Ricavando e sostituendola nella (10) si ottiene:
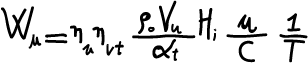
(11)
ma il rapporto è la superficie
dello stantuffo, quindi:
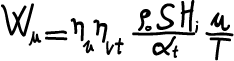
(12)
Moltiplicando la formula sopra per il numero di cilindri si ottiene la formula della potenza per motori pluricilindrici:
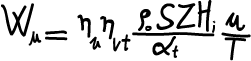
(13)
dove è la superficie totale degli stantuffi.
Una prima considerazione da fare è che quando si fa comparire la velocità media dello stantuffo la potenza utile erogata dal motore non dipende dalla cilindrata ma dalla superficie utile dei pistoni!
Andiamo adesso ad introdurre una serie di rendimenti che torneranno successivamente utili per ri-definire la formula della potenza totale.
Rendimento di intrappolamento : è il rapporto tra la massa di combustibile – ossia calore – realmente presente del cilindro al momento della combustione
e la massa di combustibile – ossia calore – effettivamente spesa ad ogni ciclo:
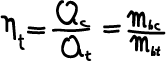
(14)
In sostanza il rendimento di intrappolamento tiene conto dei fenomeni rifiuto del combustibile.
Rendimento di combustione della camera di combustione: non tutto il calore relativo alla massa di combustibile all’interno del cilindro può essere liberato in quanto la combustione può essere incompleta. Si tiene quindi conto di questa perdita che è calcolata dal rapporto tra il calore
effettivamente liberato dalla combustione ed il calore corrispondente alla completa combustione della massa di combustibile
che si trova all’interno del cilindro.
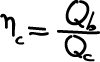 (15)
(15)
Rendimento di adiabaticità della camera di combustione: non tutto il calore generato dalla combustione partecipa al ciclo. Una parte viene perduta durante la combustione in quanto ceduta per convezione alle pareti della camera. Questo rendimento viene calcolato come rapporto tra il calore
che effettivamente partecipa al ciclo e il calore
che è effettivamente generato dalla combustione.
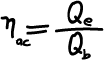
(16)
Rendimento ideale del ciclo: è calcolato come il rapporto tra il lavoro del ciclo ideale
ed il calore
che effettivamente partecipa al ciclo
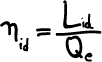 (17)
(17)
Rendimento limite del ciclo: questo fattore tiene conto della variabilità delle costanti fisiche del fluido operante (prevalentemente variazioni di temperatura e pressione). Questo viene calcolato come il rapporto tra il lavoro
fornito dal ciclo limite ed il lavoro
fornito dal ciclo ideale:
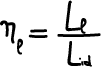 (18)
(18)
Rendimento indicato positivo è calcolato come il rapporto tra il lavoro
fornito dalla parte positiva fornita dal diagramma P-V ed il lavoro
fornito dal ciclo limite.
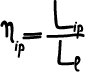 (19)
(19)
Rendimento di pompaggio : questo termine tiene conto dell’influenza del ciclo di pompaggio ed è definito come rapporto tra il lavoro totale
fornito dal ciclo completo (compreso il ciclo di pompaggio) ed il lavoro
fornito dal solo ciclo indicato positivo.
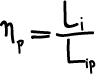
(20)
Rendimento organico: questo termine tiene di conto degli attriti degli organi meccanici all’interno del motore e dal “trascinamento” di eventuali accessori come pompa acqua e olio, generatore elettrico… Quindi il lavoro utile che viene raccolto dall’albero motore è inferiore al lavoro indicato. Si definisce quindi il rendimento organico il rapporto tra il lavoro utile disponibile sull’albero di uscita del motore a valle degli accessori ed il lavoro indicato completo:

(21)
Raccogliamo adesso tutti i termini appena discussi per definire l’espressione analitica del lavoro utile :
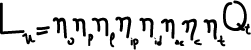
(22)
Definiamo il rendimento utile come:

(23)
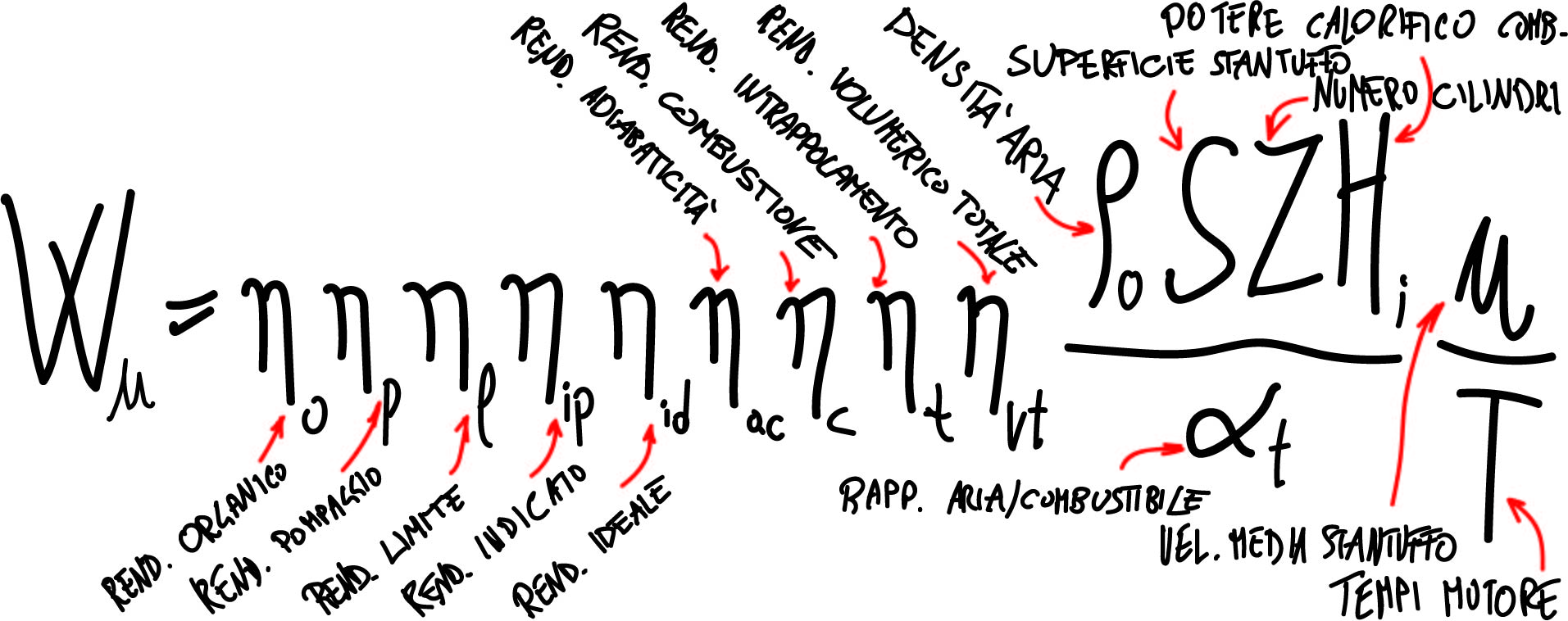
Infine sostituendo la (23) nella (13) si ottiene sua Maestà la formula della potenza utile erogata dal motore:
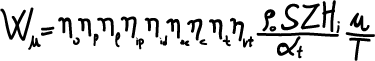
[1] “Motori ad alta potenza specifica” – Aut: Giacomo Augusto Pignone e Ugo Romolo Vercelli (questo articolo è tratto da questo testo sul quale potrete trovare innumerevoli approfondimenti sulla formula della potenza sopra descritta)

Scrivi un commento